60 分钟搞定 Tarjan 算法求解无向图的割点与桥

本人在学习 Tarjan 算法求解无向图的割点与桥的问题时，很快发现了一篇简洁易懂的文章。很顺利地了解算法的思路，并写出了“高效”的代码，此时内心飘过 —— So Easy。然而，当我翻开《算法竞赛进阶指南》这本书的有关篇章时，我发现其中经过精简优化的代码有几条语句让我不得其所。以至于，花了较多心思和时间来思考🤔这段真正高效的 Tarjan 算法的工作原理以及代码的编写。

关于 Tarjan 算法，我将会写若干篇系列文章，来完整系统地介绍 Tarjan 算法的原理以及其主要解决的问题。而在本章我主要讲一个问题 —— 如何使用 Tarjan 算法求解无向图的割点与桥。

在讲述问题之前，我们先来简单地了解下什么是 Tarjan 算法？

Tarjan 算法

Tarjan 算法是基于深度优先搜索的算法，用于求解图的连通性问题。Tarjan 算法可以在线性时间内求出无向图的割点与桥，进一步地可以求解无向图的双连通分量；同时，也可以求解有向图的强连通分量、必经点与必经边。

如果，你对上面的一些术语不是很了解，那么也毫无关系。目前为止，我们只要知道 Tarjan 算法是基于深度优先搜索的，用于求解图的连通性问题的算法就好了。

提到 Tarjan，不得不提的就是算法的作者 —— Robert Tarjan。他可是一名著名的计算机科学家，我们耳熟能详的最近公共祖先（LCA）问题、强连通分量问题、双连通分量问题的高效算法都是由他发现并解决的，同时他还参与了开发斐波那契堆、伸展树的工作。

无向图的割点与桥

首先，什么是无向图？简单说，若一个图中每条边都是无方向的，则称为无向图。

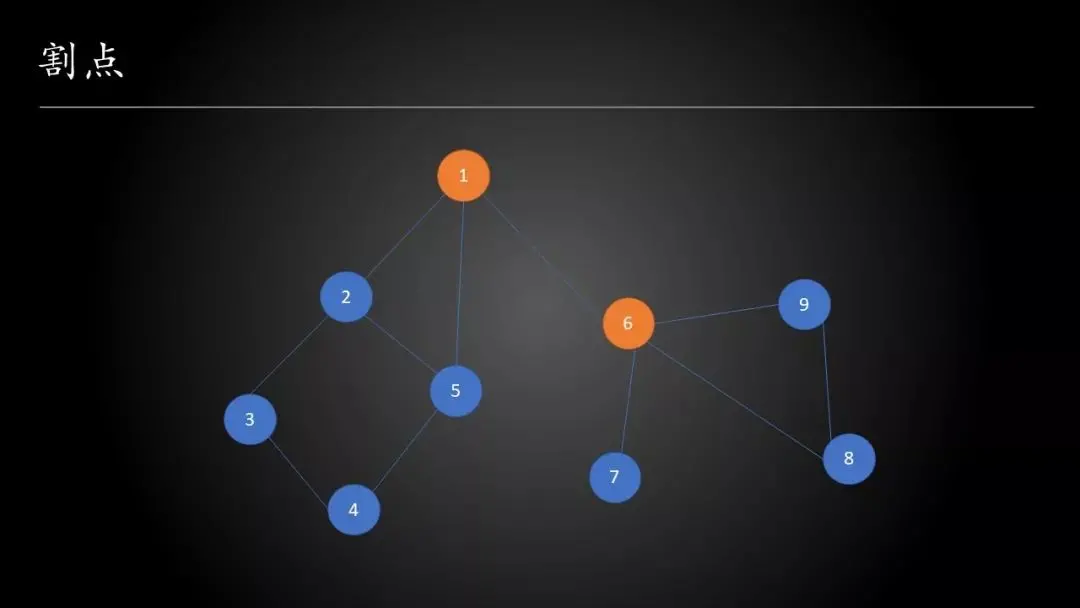
割点

若从图中删除节点 x 以及所有与 x 关联的边之后，图将被分成两个或两个以上的不相连的子图，那么称 x 为图的割点。

无向图的割点
无向图的割点

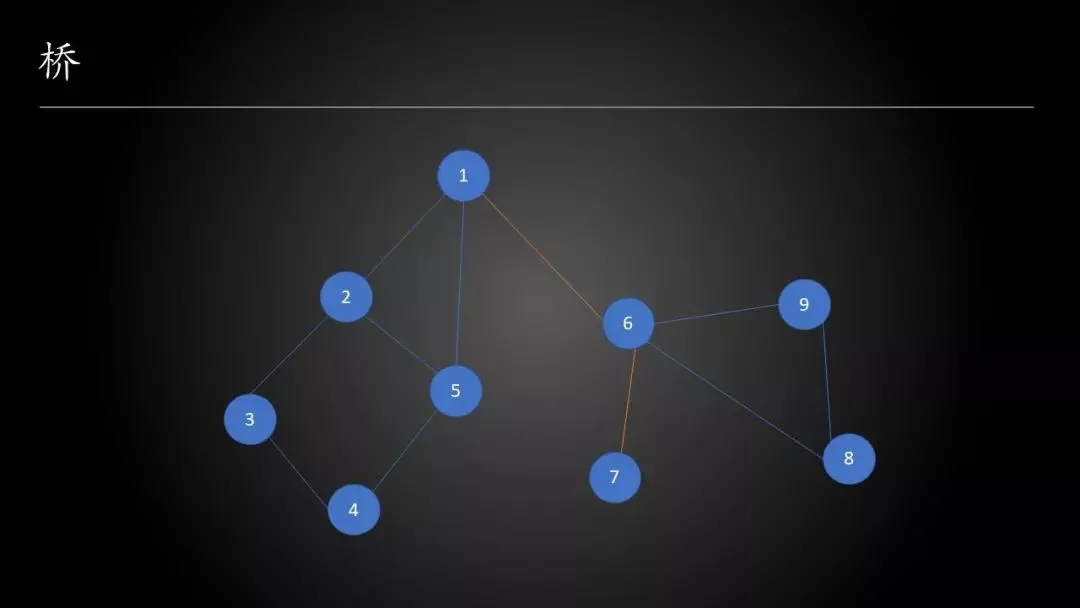
桥

若从图中删除边 e 之后，图将分裂成两个不相连的子图，那么称 e 为图的桥或割边。

无向图的桥
无向图的桥

如何求解图的割点与桥？

那么，在了解了 Tarjan 算法的背景以及图的割点与桥的基本概念之后，我们下面所面临的问题就是 —— 如何求解图的割点与桥？

在这里，我们开门见山，直接引出 Tarjan 算法在求解无向图的割点与桥的工作原理。

时间戳

时间戳是用来标记图中每个节点在进行深度优先搜索时被访问的时间顺序，当然，你可以理解成一个序号（这个序号由小到大），用 dfn[x] 来表示。

搜索树

在无向图中，我们以某一个节点 x 出发进行深度优先搜索，每一个节点只访问一次，所有被访问过的节点与边构成一棵树，我们可以称之为“无向连通图的搜索树”。

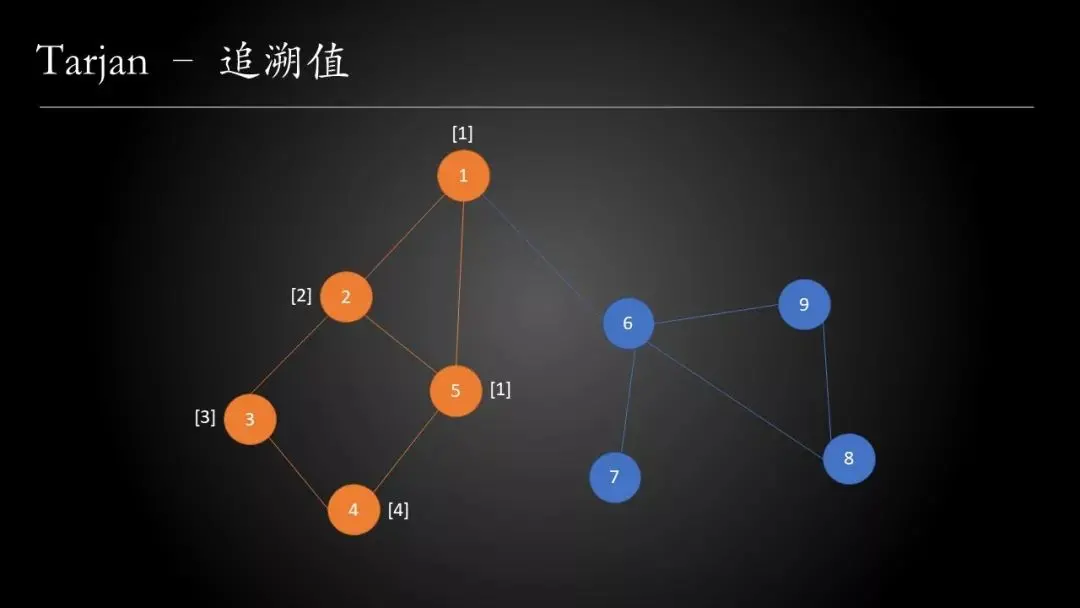
追溯值

追溯值用来表示从当前节点 x 作为搜索树的根节点出发，能够访问到的所有节点中，时间戳最小的值 —— low[x]。那么，我们要限定下什么是“能够访问到的所有节点”？，其需要满足下面的条件之一即可：

  • 以 x 为根的搜索树的所有节点
  • 通过一条非搜索树上的边，能够到达搜索树的所有节点

是的，你可能觉得这段话太绕了，那么我们通过动画的方式来摸你追溯值真实计算过程。

Tarjan 算法 —— 追溯值的计算过程

在上面的计算过程中，我们可以认为以序号 2 为根的搜索树的节点有 \{2,3,4,5\}。上面所说的“通过一条非搜索树上的边”可以理解成动画中的 (1, 5) 这条边，“能够到达搜索树的所有节点”即为节点 1。

Tarjan —— 追溯值的计算过程
Tarjan —— 追溯值的计算过程

代码详解

在了解了 Tarjan 算法的基本概念与操作流程之后，我们来看看具体的代码。说实话，在看到这一份李煜东大佬写的代码时，尽管我知道 Tarjan 在求解无向图的桥与割点的思路，也知道每一条代码语句的含义，但就是不知道为什么这样写能搞达到要求的效果。也就是说，这份代码是经过精心设计与优化后的代码。

无向图的桥判定法则

在一张无向图中，判断边 e（其对应的两个节点分别为 u 与 v）是否为桥，需要其满足如下条件即可：

dfn[u] < low[v]

它代表的是节点 u 被访问的时间，要优先于（小于）以下这些节点被访问的时间 —— low[v]。

  • 以节点 v 为根的搜索树中的所有节点
  • 通过一条非搜索树上的边，能够到达搜索树的所有节点（在追溯值内容中有所解释）

是不是上面的两个条件很眼熟？对，其实就是前文提到的追溯值 —— low[v]。

Code

// tarjan 算法求无向图的桥
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>

using namespace std;

const int SIZE = 100010;
int head[SIZE], ver[SIZE * 2], Next[SIZE * 2];
int dfn[SIZE], low[SIZE];
int n, m, tot, num;
bool bridge[SIZE * 2];

void add(int x, int y) {
    ver[++tot] = y, Next[tot] = head[x], head[x] = tot;
}

void tarjan(int x, int in_edge) {
    dfn[x] = low[x] = ++num;
    for (int i = head[x]; i; i = Next[i]) {
        int y = ver[i];
        if (!dfn[y]) {
            tarjan(y, i);
            low[x] = min(low[x], low[y]);
            if (low[y] > dfn[x])
                bridge[i] = bridge[i ^ 1] = true;
        }
        else if (i != (in_edge ^ 1))
            low[x] = min(low[x], dfn[y]);
    }
}

int main() {
    // [[0,1],[1,2],[2,0],[1,3]]
    cin >> n >> m;
    tot = 1;
    for (int i = 1; i <= m; i++) {
        int x, y;
        scanf("%d%d", &x, &y);
        add(x, y), add(y, x);
    }
    for (int i = 1; i <= n; i++)
        if (!dfn[i]) tarjan(i, 0);
    for (int i = 2; i < tot; i += 2)
        if (bridge[i])
            printf("%d %d\n", ver[i ^ 1], ver[i]);
}

当时，就是这份代码我花了不少的时间和精力琢磨，甚至还在白板上模拟演练了一把。功夫不负有心人，我终于搞懂了这一段经过精心优化过后的代码。

首先，我们来看看变量的含义。

const int SIZE = 100010;
int head[SIZE], ver[SIZE * 2], Next[SIZE * 2];
int dfn[SIZE], low[SIZE];
int n, m, tot, num;
bool bridge[SIZE * 2];
  • SIZE —— 节点的个数，可以基于实际的节点个数曾加一些冗余度
  • 关于 head/Next/ver 变量的介绍，可以参阅下面的动画配合理解
    • 假设场景，有一个节点 u，以及其直接相连的若干节点 v1, v2, v3
    • head[u] 代表节点 u 直接相邻的第一个节点 v1 的序号（tot1）
    • Next[tot1] 代表节点 u 直接相邻的下一个节点的序号（tot2）
    • ver[tot1] 代表序号为 tot1 的节点的值（v1）
  • dfn[x] 代表节点x对应的时间戳，low[x] 代表节点 x的追溯值
  • n 与 m 代表程序的标准输入的参数，n 代表节点的个数，m 代表边的个数
  • tot 代表每一个节点的序号
  • num 代表每一个节点的时间戳
  • bridge[tot] 代表序号为tot 的边是否为桥

针对于 head、Next、ver 变量的关系还是比较难懂。那么，我们用图像的方式，把节点 u、v1、v2 与 v3 画出来看看。

Tarjan —— head next ver 变量关系
Tarjan —— head next ver 变量关系

通过上图我们可以形象地理解这三个变量之间的关系。那么，针对于 add 方法，想必也可以很顺利地想明白 —— 建立并维护节点 x、y 形成的边。

接着，我们看看 Tarjan 算法的主体

// x 代表当前搜索树的根节点，in_edge 代表其对应的序号（tot）
void tarjan(int x, int in_edge) {
    // 在搜索之前，先初始化节点 x 的时间戳与追溯值
    dfn[x] = low[x] = ++num;
    // 通过 head 变量获取节点 x 的直接连接的第一个相邻节点的序号
    // 通过 Next 变量，迭代获取剩下的与节点 x 直接连接的节点的序号
    for (int i = head[x]; i; i = Next[i]) {
        // 此时，i 代表节点 y 的序号
        int y = ver[i];
        // 如果当前节点 y 没有被访问过
        if (!dfn[y]) {
            // 递归搜索以 y 为跟的子树
            tarjan(y, i);
            // 计算 x 的追溯值
            low[x] = min(low[x], low[y]);
            // 桥的判定法则
            if (low[y] > dfn[x])
                bridge[i] = bridge[i ^ 1] = true; // 标记当前节点是否为桥（具体见下文）
        }
        else if (i != (in_edge ^ 1)) // 当前节点被访问过，且 y 不是 x 的“父节点”（具体见下文）
            low[x] = min(low[x], dfn[y]);
    }
}

语句一：i != (in_edge ^ 1)

在我第一次看到这句代码时，我满脑子都是 —— “这是个啥？”

问题还是需要解决，冷静一下~。

首先，我们先明确下“y 不是 x 的父节点”的情况是什么？

Tarjan “父节点”的判定

如上面的视频的过程，首先以 x' 节点出发进行深度优先搜索，紧接着搜索到节点 x。此时，以 x 为根进行递归搜索，计算出其下一个节点为 y。如何此时 y 与 x' 是一个节点的话 —— y 是 x 的“父节点”，需要忽略这种情况对于追溯值的计算。

我们知道，在建立边的关系时（add），我们为每一条边的两个节点创建了两个相邻的序号值。又因我们 tot 是从 2 开始计数的，故每一条边的两个节点的序号肯定是一奇一偶，偶数为小。比如，2 与 3，4 与 5 ，而不会出现 5 与 6 这样的情况。

在明确了上面的情况之后，我们看看一个数 x 与 1 进行异或的结果是什么？

  • 如果 x 为偶数（2），那么 x \wedge 1 = 2 \wedge 1 = 3
  • 如果 x 为奇数（3），那么 x \wedge 1 = 3 \wedge 1 = 2

最后，我们来想想如何判定两个点是否属于一条边的两个端点？是不是只要满足 a \wedge 1 == b 条件，那么 a 与 b 就是一条边的两个端点了？对，就是这样！

语句二：bridge[i] = bridge[i ^ 1] = true

这句话是为了标记某个节点对应的边是桥。而又因为我们在建立边时是成对地，那么相邻的两个节点都应该被标记。

实践题

LeetCode-cn：https://leetcode-cn.com/problems/critical-connections-in-a-network/（查找集群内的「关键连接」）

这道题描述的非常直接 —— 求解无向图的桥，大家可以试试使用上述的Tarjan算法进行求解。

上面的代码，大家可以保留下来作为一个模板来学习或使用。

总结

想必通过对 Tarjan 算法的基本概念，无向图以及其桥与割点的概念，Tarjan 算法求解桥与割点的代码的详细介绍，大家已经能够掌握了这个知识点。

在学习 Tarjan 算法的过程中，我进入到了无法理解代码的窘境。代码就在我面前，然而它认识我我不认识它。面对这样的窘境，我的方式就是使用一个简单的例子，在白板上进行一个简单的模拟演练，把代码的执行过程可视化形象化。希望，大家在遇到类似的情况时，能够借鉴这种方式来解决自己的问题。

最后留一道思考题：无向图的桥与割点的判定在实际生活中有哪些应用？可以在下方留言

本文首发于 [LeetCode力扣] 微信公众号

Tags:
Share:

Leave a Reply

Your email address will not be published. Required fields are marked *

This site uses Akismet to reduce spam. Learn how your comment data is processed.