递归是什么?
递归(英语:Recursion),又译为递回,在数学与计算机科学中,是指在函数的定义中使用函数自身的方法 。
维基百科
简单说,就是自身调用自身。
为什么使用递归?
往往面对一类问题时,如果它的规模足够小或者说达到既定的边界条件时,我们可以直接获取答案。但是,当这类问题的规模比较大时,却往往无法直接获取答案。那么,这个时候就可以通过“自身调用自身”的方式,来不断地减小问题的规模,直到问题的规模被缩减到足够小时,直接将答案返回上层的调用者,最终获取到原问题的解。如果将求解的过程逆过来,那么就是所谓的递推。
通过这种方式,我们可以写出“优雅”的代码去解决规模比较大的问题。进而,避免了通过递推的方式,在每一次递推时产生的复杂的条件判断的问题。
上文中提到经过递归调用,会不断地减小问题的规模,有些作者认为这是一种减治法。
递归的特性
自身调用自身
在上文中,已经提到了这个特性,而且也非常好理解,不再赘述。
回溯时还原现场
在使用递归方法时,其中有一个不得不提的特性——回溯时还原现场。
通过递归调用,程序将执行到极限触达边界条件时,就需要将当前层的调用跳出“调用栈”,在跳出“调用栈”时,需要将一些状态信息还原到上一层场景所属的状态,即所谓的回溯时还原场景。
举个例子
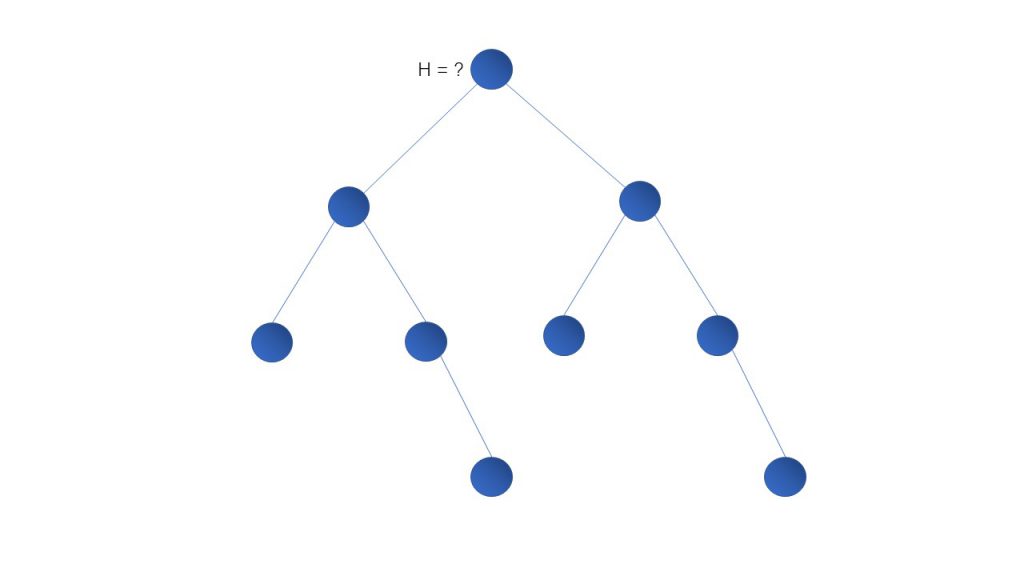
有一颗二叉树,求解h(root)。h(root)代表以root为根的树的最大高度,即h(root) = max(h(root->left), h(root->right))。
首先,我们要定义一个递归函数。在定义函数之前,我们要明确两个重要的事情:
- 函数的含义 —— 返回值
- 函数的参数
函数的含义,代表了递归函数能为我们解决什么样的问题。在这里,我们定义函数的含义为求解某一个子树的高度。
函数的参数,代表了递归函数求解的问题的规模。在这里,我们定义函数的参数为当前需要遍历的节点 —— 以当前节点为根的子树(问题规模)。
在明确了这两件事情之后,面对一个规模较大的、复杂的问题就会变的简单得多。
下面,我们来看看在使用递归函数解决当前问题的整个过程。
- 蓝色 —— 代表未访问过的节点
- 橘色 —— 代表当前调用栈中正在遍历的节点
- 灰色 —— 代表已经访问过,且不再当前调用栈正在遍历的节点中的节点
记忆化递归
通过上面简单的例子,我们了解了如何通过递归解决一个较大规模的问题。但是,我们会发现,使用递归函数解决的每个子问题的解仅仅被使用了一次。然而,在某些复杂的场景,子问题的解可能被使用若干次。那么这个时候,可以考虑加上备忘录法进行优化,即记忆化递归。
递归 —— 这种方法的思考方式是自顶向下的,也就是说符合我们常人在解决问题时的正向思考的过程。这与动态规划 —— 自底向上的方法恰恰相反(记忆化递归与动态规划的问题,我将在后续的篇章中讲解)。
三个经典问题
递归实现指数型枚举
从 1 ~ n 这 n(n < 20) 个整数中随机选取任意多个,输出所有可能的选择方案。
在最开始学习算法时,面对这种类似的问题我思考了好久。当打开大牛的代码时,才恍然大悟,原来可以用这么简洁的代码解决 —— 递归。
那么,先来分析下这个“小”问题。我们需要在一个序列中1, 2, 3, ...\ 19, 20随机选取任意多个数字,也就是说每一个数字都有两种可能——选择或不选择。那么,一共的可能的方案总数即 —— 2 ^ n
那么,根据上文提到的方案,我们先来确认两件事情:
- 函数的含义 —— 输出所有可能的方案
- 函数的参数 —— int x,代表问题的规模是[x, n]的区间。
明确这两件事情之后,我们还需要一个额外的全局变量(vector<int> results),用来保留递归过程中产生的状态信息 —— 当前调用栈被选中的数字。
#include <iostream>
#include <vector>
using namespace std;
const int N = 20;
void helper(vector<int>& results, int s) {
// 边界情况
if (s == N + 1) {
// 在到达问题边界时,直接将选择的数字输出即可
for (auto& n : results) {
cout << n << " ";
}
cout << endl;
return;
}
// 选择当前数字
results.push_back(s);
helper(results, s + 1); // 求解规模更小的子问题
results.pop_back(); // 在回溯到上一个问题时,需要还原现场
// 不选择当前数字
helper(results, s + 1); // 求解规模更小的子问题
}
int main() {
vector<int> results{};
helper(results, 1);
}时间复杂度
O(2^n) 每一个数字有两种可能 —— 选择或不选择
递归实现组合型枚举
从 1 ~ n 这 n(n < 20) 个整数中随机选出 m(0<=m<=n<=20)个,输出所有可能的选择方案。
这个问题与上面的问题的唯一区别是限定了选定元素的个数m。
很自然地我们可以想到,在输出答案时我们只需要判断下结果集变量 —— results的大小是不是m即可。当然,我们也可以在每次搜索时进行判断 —— 剪枝法,这样可以带来性能上的提升。
#include <iostream>
#include <vector>
using namespace std;
const int N = 20;
const int M = 4;
void helper(vector<int>& results, int s) {
// 边界情况
if (results.size() > M || results.size() + N - s + 1 < M) {
// 剪枝
return;
}
if (s == N + 1) {
// 在到达问题边界时,直接将选择的数字输出即可
for (auto& n : results) {
cout << n << " ";
}
cout << endl;
return;
}
// 选择当前数字
results.push_back(s);
helper(results, s + 1); // 求解规模更小的子问题
results.pop_back(); // 在回溯到上一个问题时,需要还原现场
// 不选择当前数字
helper(results, s + 1); // 求解规模更小的子问题
}
int main() {
vector<int> results{};
helper(results, 1);
}时间复杂度
O(C^{m}_{n})我们可以通过判断当前调用栈中的results中的数字个数如果大于M,或者加上剩余的所有数字都达不到M个的话,那么直接返回,跳出调用栈,进行其他情况的搜索。这样,避免了无谓的搜索,只关心满足条件的结果集。所以时间复杂度就从 O(2^n) 降到了 O(C^{m}_{n})。
递归实现排列型枚举
把 1 ~ n 这 n(n < 10) 个整数排成一行后随机打乱顺序,输出所有可能的选择方案 —— 全排列问题。
现对于求解组合问题,全排列问题的最大的区别是要保留每个选中的数字之间的顺序。
为了保留选择的顺序,我们需要一个标记是否访问过的数组vector<bool> visited。
#include <vector>
using namespace std;
const int N = 10;
vector<bool> vis(N, false);
vector<int> result{};
void helper() {
if (result.size() == N) {
// 在到达问题边界时,直接将选择的数字输出即可
for (auto& n : result) {
cout << n << " ";
}
cout << endl;
return;
}
for (int i = 0; i < N; ++i) {
// 每一次选择未被访问过的数字
if (vis[i]) continue;
// 选择当前数字
vis[i] = true;
result.push_back(i + 1);
helper(); // 递归求解子问题
// 在回溯到上一个问题时,需要还原现场
result.pop_back();
vis[i] = false;
}
}
int main() {
helper();
return 0;
}时间复杂度
O(n!)在第一次选择数字时,有n种选择,接着有n - 1种选择,直到剩最后一个元素时就剩1种选择,故时间复杂度 —— 方案数为:n * (n -1) * (n -2) * ... * 2 * 1 = n!
思考题
上面,我们用递归实现了三个问题——指数型枚举,组合型枚举以及全排列问题。那么,针对于排列问题,如果期望在1 — n的序列中找到元素个数为m的所有排列的情况该如何做呢?
最后,能否找出利用递归求解组合和排列时的区别与共性呢?我想如果能够牢记其区别与共性,那么这类问题就会变得异常简单。
LeetCode 相关题目
- 组合型枚举:https://leetcode-cn.com/problems/combinations/
- 全排列:https://leetcode-cn.com/problems/permutations/
